From Silicon Labs: "Six-Degrees of Separation"

It has been postulated that every human is connected to every other human with only six relationships between. It has also been proven that probabilistically, you can be in a room with 23 people and have a 50 percent chance of two people having the same birthday. These connections are all around us. It turns out that digital electronic frequencies seem to have an even tighter relationship when viewed by their fractional relationships.

Rational numbers are numbers that can be written it the form of a + b/c where a, b, & c are all integers. This is a handy way to work with frequencies because of the extensive relationships we have found between seemingly unrelated applications.

Fractional Relationships

At Silicon Labs, we see a lot of seemingly unique frequencies from our customers. Consequently, we are in a prime spot to observe relationships between frequencies.

Recently, we received a request for a Si5338 frequency plan that had the following frequencies:

Input: 185.439560440 MHz

OUT1: 148.5 MHz

OUT2: 148.351648352 MHz

OUT3: 27 MHz

Upon initial inspection, there are no nice fractional relationships between these numbers. When such complex divider values are needed, it limits the ability of our algorithms to optimize the performance. So, we dug in a bit to understand the real source of these high-precision numbers.

First, we noted that some of these frequencies look to be related to the SMPTE standard where the line data rate can be 1485Mbps or 2970Mbps. 27MHz is also used by SMPTE systems. In SMPTE, the fraction 1000/1001 is deployed to avoid interference.

Armed with the customer’s entered frequencies and our knowledge of the SMPTE standards, we begin our detective work:

185.439560440 * 1001/1000 = 185.62500000044

If we can truncate those last two digits, we would have a nice fractional value, but where did those odd values come from. Let’s truncate and find out. Often, we are looking to get to a line rate of something we have seen before. To do so, we often see line rates that are multiples of the clocks by factors of 2, 4, 8, 16, 10, or 20.

185.625000000 * 2 = 371.25

185.625000000 * 4 = 742.5

185.625000000 * 8 = 1485

185.625000000 * 16 = 2970

185.625000000 * 10 = 1856.25

185.625000000 * 20 = 3712.5

Here we have found two SMPTE-related numbers 1485 and 2970. Eureka! So:

185.439560440 is better written as 2970/16/1001*1000 or 185.4395604 4395604 4395604 (repeating)

Armed with our new knowledge, we can apply these fractions and base numbers to take full advantage of our frequency planning algorithms. To enter these values, we have created a frequency editor that can accept equations.

Pulling up CBPro for the Si5338, and proceeding to the input frequency page:

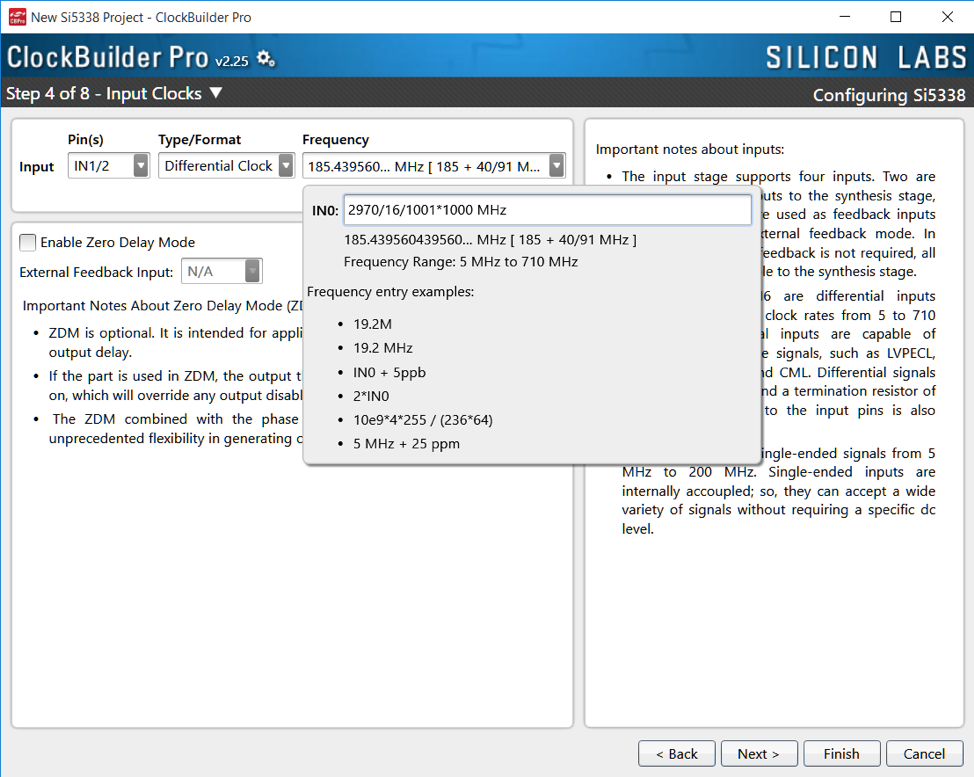
Continuing this for the outputs:

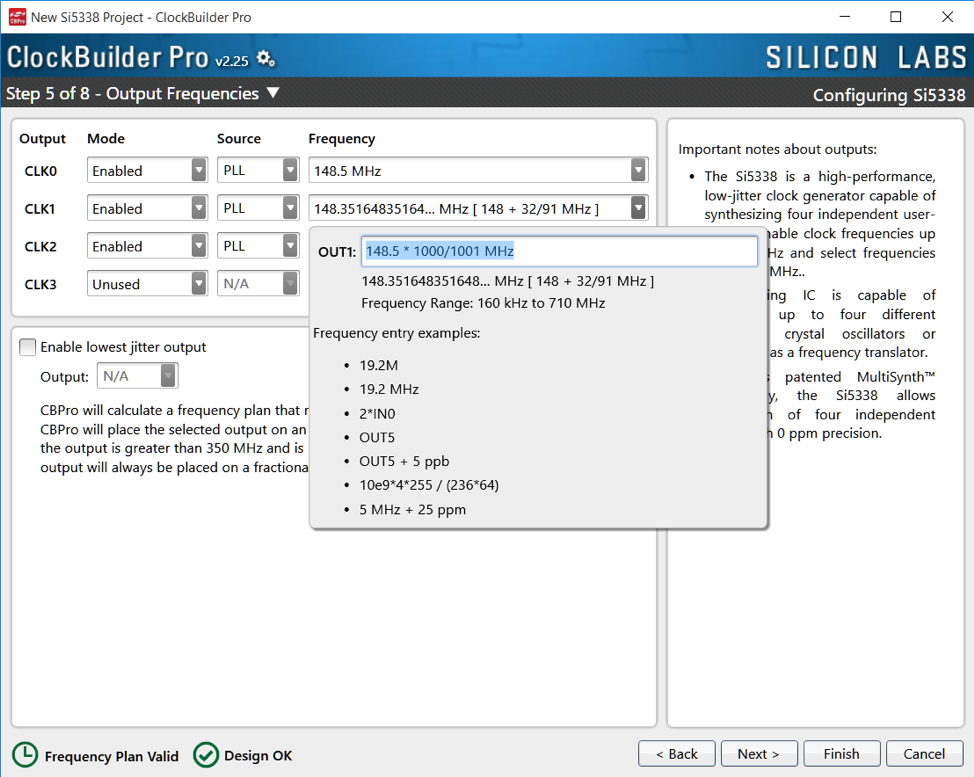
As you can see at the bottom of the window, the frequency plan is valid and the design is ok, which means it has been optimized. Entering the frequencies as they were given, yields an unrealizable plan.

This same frequency entry form is available throughout CBPro for our clock generators, jitter attenuators, and synchronization clock products.

Conclusion

By entering the input and output frequencies as the full fraction values, CBPro can best optimize to achieve the desired synchronous result (no frequency error) with the lowest jitter possible. The frequency editor in CBPro accepts multiplication, division, addition, subtraction, and even PPM addition giving you the easiest path to creating the frequencies you need in your designs. If you are unsure if the relationships exist, we are here to help you.

(CBPro can be downloaded from Silicon Labs website from http://www.silabs.com/cbpro)

Source: https://www.silabs.com/community/blog.entry.html/2018/07/19/six-degrees_of_separ-rlLk